ALmoMD
User Manual
For the input fiels and parameters, please check below links.
Theoretical Background
Active-learning machine-operated molecular dynamics (ALmoMD) is a Python code package designed for the effective training of machine learned interatomic potential (MLIP) through active learning based on uncertainty evaluation. It also facilitates the implementation of molecular dynamics (MD) using trained MLIPs with uncertainty evaluation.
Uncertainty Evaluation
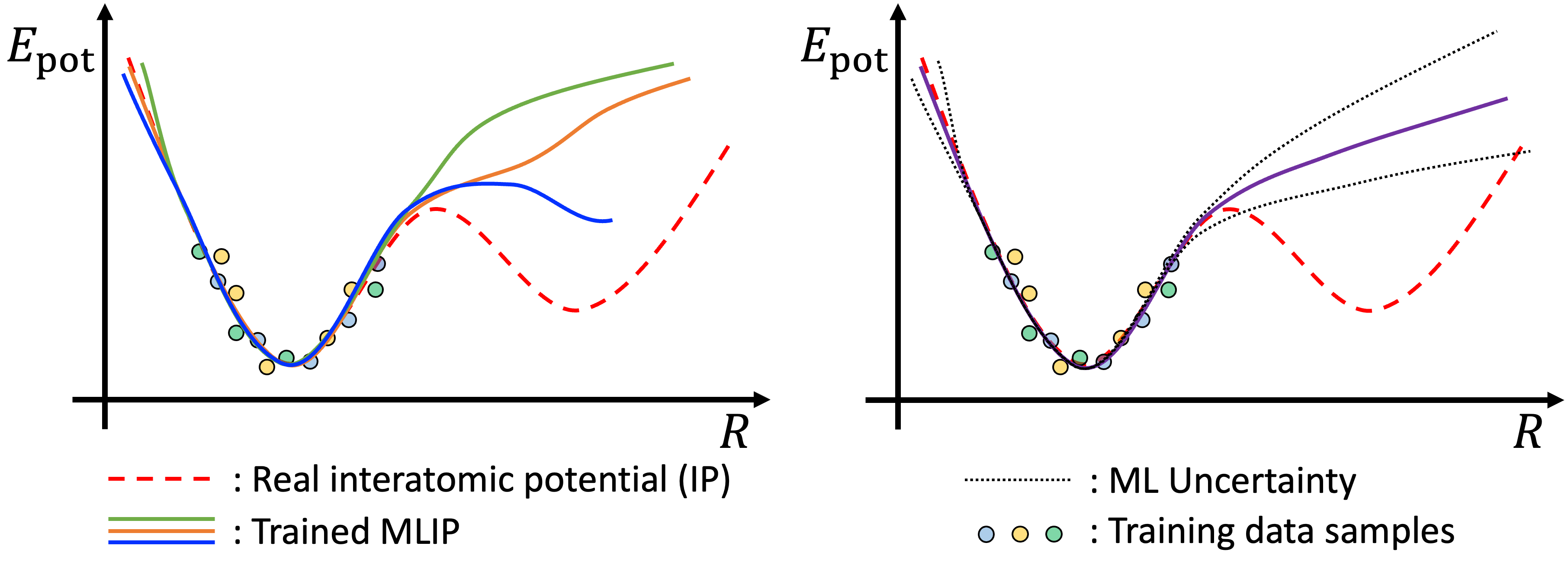
In ALmoMD, uncertainty refers to the prediction uncertainty of a group of trained models, which can be obtained through three distinct training methods [1]. First, each model can be trained with the same number of different training data (Subsampling). Second, each model can be trained with different random initializations of the machine learning model but the same training data (Deep Ensemble). Lastly, each model can be trained using different machine learning techniques. In each case, as displayed in Fig. 1, these models provide a range of different predictions, and their standard deviation indicates the degree of uncertainty, which is used in active learning. ALmoMD combines Subsampling and Deep Ensemble methods to determine this uncertainty.
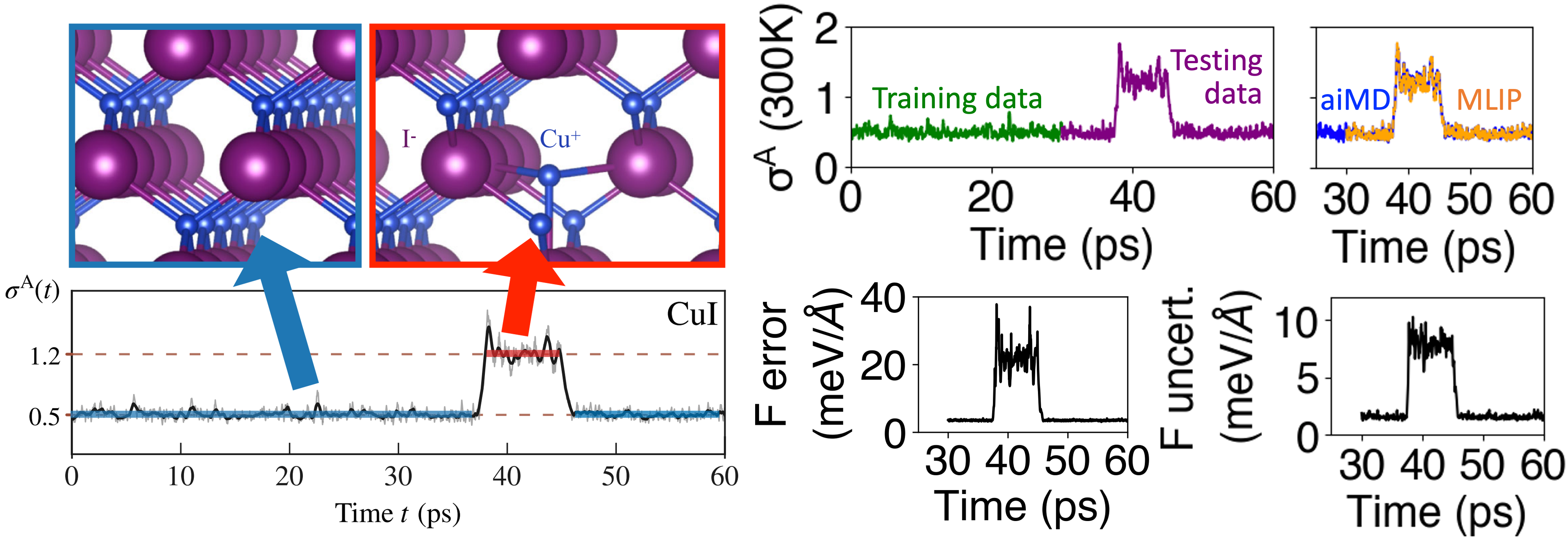
We note that there are significant concerns regarding the use of uncertainty in global phase predictions, as raised by both the Zipoli group [1] and Scheffler group [2]. However, in ALmoMD, we utilize uncertainty to qualitatively identify cases when the models go beyond their trained domain, enabling us to determine where additional model training is necessary. For instance, consider CuI [3], which exhibits a rare dynamical event involving defect creation, as illustrated in Fig. 2. Due to the challenging nature of ab initio MD, there’s a possibility of terminating it before experiencing this event, for example, at 30 ps. In such cases, we train the MLIP using only the green trajectory of anharmonicity [4] shown in Fig. 2. When we subsequently test these trained models with the purple trajectory, which includes states with defects, it results in significant spikes in errors and uncertainties (as seen in the forces in Fig. 2). Therefore, we can qualitatively employ uncertainty as a means of identifying when MD departs from its trained regime.
Active Learning Scheme
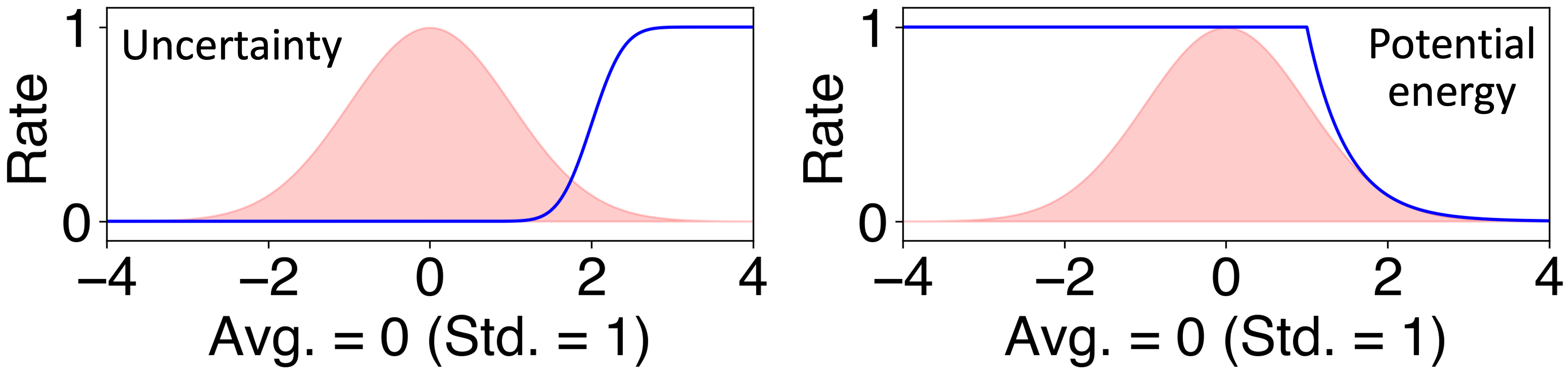
ALmoMD facilitates the qualitative identification of uncertainty to sample the next round of training data. Uncertainty can be evaluated in terms of potential energy, forces on atoms, and the degree of anharmonicity. Particularly for forces, uncertainty can be determined as either its average or its maximum value. On the other hand, ALmoMD rejects candidate data when it exhibits excessive potential energy, which is unphysical. This can occur when using molecular dynamics with poorly trained MLIP, leading to a flawed trajectory. In detail, ALmoMD employs two soft criteria concerning uncertainty and potential energy. First, the probability criterion for uncertainty is defined as follows:
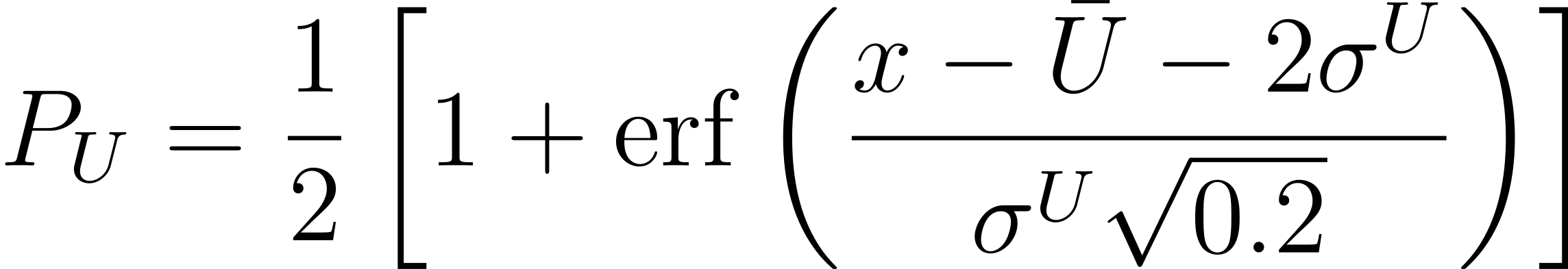
where $\bar{U}$ and $\sigma^{U}$ represent the average and standard deviation of the uncertainty in the testing data. This equation is based on an accumulated Gaussian distribution. Second, the probability criterion for potential energy is defined as follows:
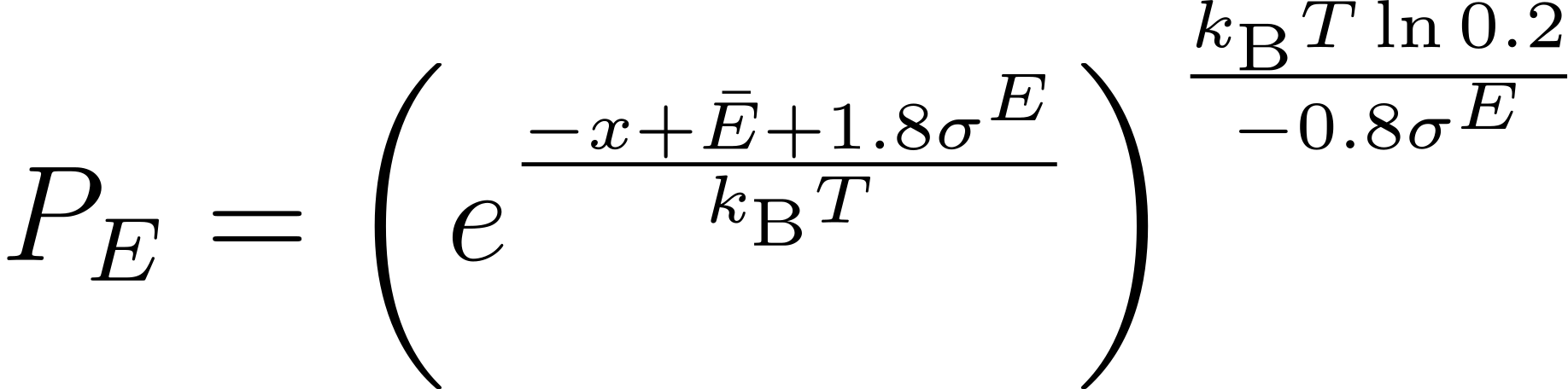
where $\bar{E}$ and $\sigma^{E}$ represent the average and standard deviation of the potential energy in the testing data. This equation originates from the probability of the canonical ensemble.
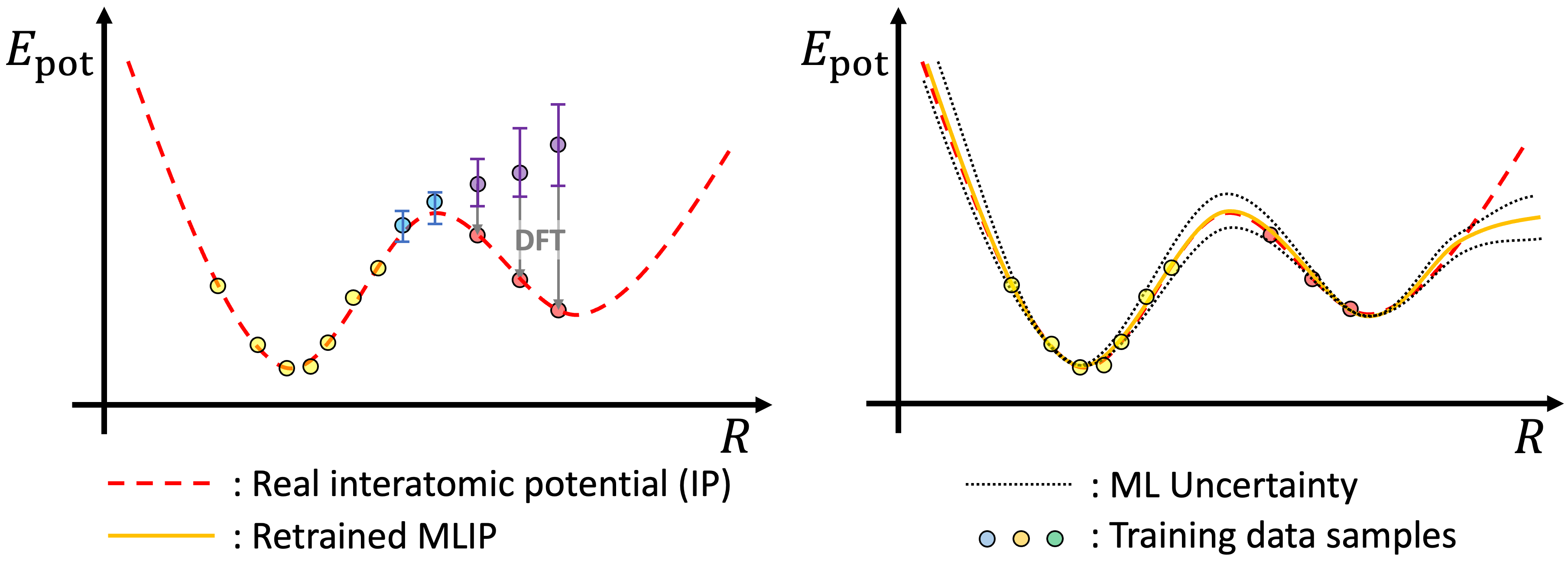
Once next round of training data with high uncertainty are sampled, they go through DFT calculations and they are added to previous list of training data. Then, prediction of newly trained model will provide corrected potential energy surface. This active learning is implemented iteratively, and each iterative step will give more reliable prediction.
Key Summary
The key advantage of ALmoMD is
- train the MLIP model without implementation of challanging ab initio molecular dynamics,
- pinpoint next round of training data qualitatively based on high uncertainty of prediction,
- and effectively explore the potential energy surface using MD with MLIP, which enabling the capture of rare dynamical events.
References
- [1] L. Kahle and F. Zipoli, Phys. Rev. E 105, 015311 (2022).
- [2] S. Lu, L.M. Ghringhelli, C. Carbogno, J. Wang, and M. Scheffler, arXiv:2309.00195 (2023).
- [3] F. Knoop, T. A. R. Purcell, M. Scheffler, and C. Carbogno, Phys. Rev. Lett. 130, 236301 (2023).
- [4] F. Knoop. T. A. R. Purcell, M. Scheffler, and C. Carbogno, Phys. Rev. Materials 4, 083809 (2020).